Problema

Una compañía que produce botellas de agua reporta los siguientes datos de costos:

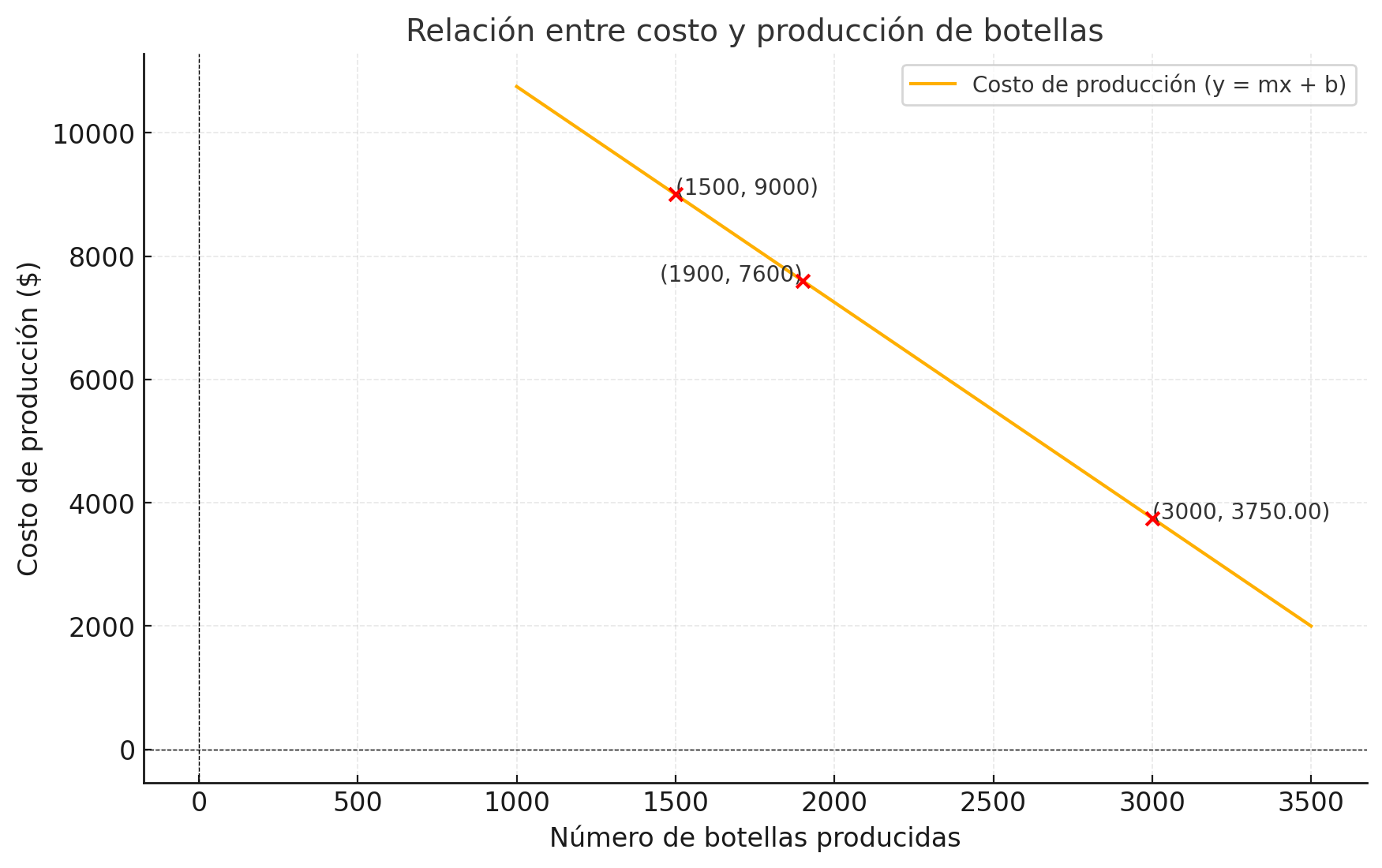
• Producción de 1,500 botellas: $9,000
• Producción de 1,900 botellas: $7,600

Sabemos que el costo varía de manera lineal con respecto a la cantidad de botellas producidas. Con base en esta información, realiza lo siguiente:

a. Encuentra la expresión matemática que describe el costo de producción.

Utiliza los puntos dados, ((1500, 9000)) y ((1900, 7600)), para determinar la ecuación de la recta que relaciona el costo ((y)) con la cantidad de botellas producidas ((x)).

b. Calcula el costo de producir 3,000 botellas.

Usa la ecuación obtenida en el inciso anterior para encontrar el costo de producción cuando (x = 3000).

c. Representa gráficamente la relación costo-producción.

Dibuja la gráfica de la ecuación obtenida para visualizar cómo el costo cambia en función de la cantidad de botellas producidas.

---

Instrucciones

1. Identifica los puntos clave: Los datos dados representan dos puntos en el plano cartesiano. Usa la fórmula de la pendiente ((m)) y la ecuación de la recta para resolver el inciso a.

2. Sustituye valores: Una vez que tengas la ecuación, reemplaza el valor de (x) por (3000) para encontrar el costo correspondiente.

3. Traza la gráfica: Representa la ecuación en un plano cartesiano, destacando los puntos dados y el punto calculado en el inciso b.

---

Solución

👉 Ver solución

a. Expresión matemática que describe el costo de producción

La ecuación de una recta es $y = mx + b$, donde:

$m$ es la pendiente:

$$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{7600 - 9000}{1900 - 1500} = -3.5$$

$b$ es la intersección con el eje $y$, calculada como:

$$b = y_1 - m \cdot x_1 = 9000 - (-3.5) \cdot 1500 = 14250$$

Por lo tanto, la ecuación es:

$$y = -3.5x + 14250$$

b. Costo para producir 3,000 botellas

Sustituyendo $x = 3000$ en la ecuación:

$$\begin{align*} y &= -3.5(3000) + 14250 \\ &= -10500 + 14250 \\ &= 3750 \end{align*}$$

El costo de producir 3,000 botellas es $3,750.

c. Gráfica de la relación costo-producción

La gráfica muestra cómo el costo varía con la producción de botellas. Los puntos destacados son:

• $(1500, 9000)$
• $(1900, 7600)$
• $(3000, 3750)$

---