Problema: Relación lineal entre variables

En un problema de geometría analítica, estamos estudiando la relación entre dos variables x e y:

Definición de variables:

• x: Variable independiente que representa la temperatura en grados Celsius (°C)
• y: Variable dependiente que representa la temperatura en grados Fahrenheit (°F)

Se conocen los siguientes pares ordenados:

• Punto 1: (0, 32) - Cuando la temperatura es 0°C, equivale a 32°F (punto de congelación del agua)
• Punto 2: (100, 212) - Cuando la temperatura es 100°C, equivale a 212°F (punto de ebullición del agua)

Con base en esta información, resuelve lo siguiente:

a. Encuentra la ecuación de la recta que relaciona y en términos de x

Determina la ecuación de la forma y = mx + b que relaciona ambas variables.

b. Calcular y cuando x = 168

Sustituye el valor de x = 168 en la ecuación y calcula el valor correspondiente de y.

c. Despeja x en términos de y y calcula x cuando y = 78

Reescribe la ecuación para obtener x = f(y) y determina el valor de x cuando y = 78.

d. ¿Para qué valor de x se cumple que x = y?

Encuentra el punto de intersección de la recta con la línea y = x.

e. Representa gráficamente la relación entre ambas variables

Dibuja la gráfica de la función y = f(x), identificando los puntos significativos.

---

Tips

1. Identifica los puntos clave: Utiliza los pares ordenados (x, y) dados para obtener los parámetros de la recta.

2. Determina la ecuación lineal: Calcula la pendiente (m) y la ordenada al origen (b) para encontrar la ecuación de la recta.

3. Evalúa la función: Utiliza la ecuación para calcular valores específicos de las variables.

4. Resuelve la intersección: Para encontrar cuando x = y, plantea un sistema de ecuaciones.

5. Traza la gráfica: Representa la relación en un plano cartesiano, marcando los puntos relevantes.

---

Solución

👉 Ver solución

a. Ecuación de la recta y = mx + b

Tenemos dos puntos conocidos:

• (0, 32): x = 0°C, y = 32°F
• (100, 212): x = 100°C, y = 212°F

La ecuación de una recta es y = mx + b, donde:

La pendiente m se calcula como:

$$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{212 - 32}{100 - 0} = \frac{180}{100} = 1.8$$

La ordenada al origen b se obtiene sustituyendo un punto conocido en la ecuación:

$$y_1 = m \cdot x_1 + b$$ $$32 = 1.8 \cdot 0 + b$$ $$b = 32$$

Por lo tanto, la ecuación de la recta es:

$$y = 1.8x + 32$$

Donde:

• y representa la temperatura en grados Fahrenheit (°F)
• x representa la temperatura en grados Celsius (°C)

b. Cálculo de y cuando x = 168

Sustituimos x = 168°C en la ecuación:

$$\begin{align*} y &= 1.8(168) + 32 \\ &= 302.4 + 32 \\ &= 334.4 \end{align*}$$

El valor de y cuando x = 168°C es y = 334.4°F

c. Expresión de x en términos de y

Partimos de la ecuación y = 1.8x + 32 y despejamos x:

$$\begin{align*} y &= 1.8x + 32 \\ y - 32 &= 1.8x \\ x &= \frac{y - 32}{1.8} \end{align*}$$

Esta nueva ecuación nos permite calcular la temperatura en Celsius (x) a partir de la temperatura en Fahrenheit (y).

Ahora calculamos x cuando y = 78°F:

$$\begin{align*} x &= \frac{78 - 32}{1.8} \\ &= \frac{46}{1.8} \\ &= 25.56 \end{align*}$$

El valor de x cuando y = 78°F es x = 25.56°C

d. Valor de x cuando x = y

Para determinar cuándo x = y (es decir, cuándo la temperatura en Celsius es igual numéricamente a la temperatura en Fahrenheit), planteamos la igualdad:

$$\begin{align*} y &= x \\ 1.8x + 32 &= x \\ 1.8x - x &= -32 \\ 0.8x &= -32 \\ x &= -40 \end{align*}$$

Por lo tanto, cuando x = -40°C, también y = -40°F. Es decir, el punto de intersección es (-40, -40).

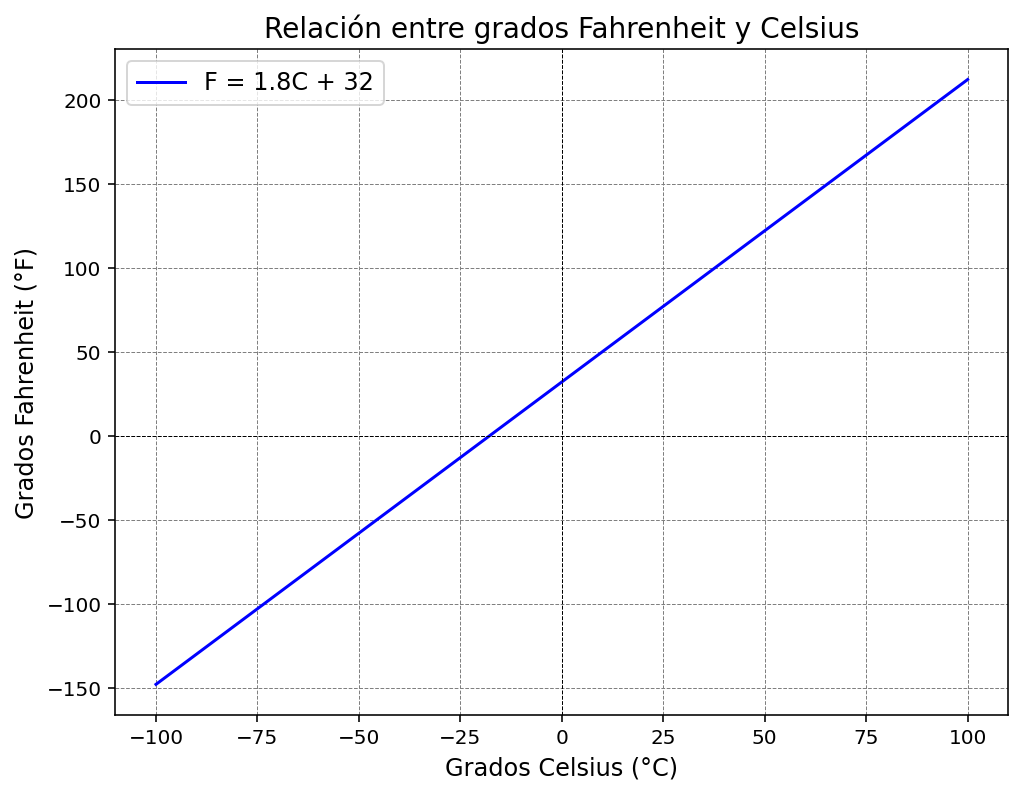
e. Gráfica de la relación entre variables

La gráfica es una línea recta con pendiente 1.8 y ordenada al origen 32. Los puntos destacados son:

• (0, 32): Punto de intersección con el eje y (cuando x = 0°C, y = 32°F)
• (100, 212): Segundo punto conocido (cuando x = 100°C, y = 212°F)
• (-40, -40): Punto de intersección con la recta y = x (cuando las lecturas coinciden)

---

Aplicaciones prácticas

Este problema ilustra cómo la geometría analítica permite modelar relaciones lineales entre variables físicas:

1. Conversión de unidades: La ecuación permite transformar valores entre diferentes sistemas de medición.

2. Modelado lineal: Muestra cómo fenómenos físicos pueden representarse mediante funciones lineales.

---